√完了しました！ (x y)^3 identity class 9 309005

Algebraic Identities Cubic Type ,Polynomials Get topics notes, Online test, Video lectures, Doubts and Solutions for CBSE Class 9 on TopperLearningFree download NCERT Solutions for Class 9 Maths Chapter 2 Exercise 21, 22, 23, 24 and 25 of Polynomials in PDF form Online sols & practice questionsRead and download free pdf of CBSE Class 9 Mathematics Polynomials Worksheet Set C Students and teachers of Class 9 Polynomials can get free printable Worksheets for Class 9 Polynomials in PDF format prepared as per the latest syllabus and examination pattern in your schools Standard 9 students should practice questions and answers given here for Polynomials in Grade 9 which will

Use A Suitable Identity To Get Each Of The Following Products I

(x y)^3 identity class 9

(x y)^3 identity class 9-Factorisation is the opposite process of expanding brackets For example, expanding brackets would require \ (2 (x 1)\) to be written as \ (2x 2\) Factorisation would be to start with \ (2x 2\) and end up with \ (2 (x 1)\) The two expressions \ (2 (x 1)\) and \ (2x2\) are equivalent;NCERT Solution For Class 9 Maths Chapter 2 Polynomials Using identity, (xyz)2 = x2y2z22xy2yz2zx Here, x = (1/4)a y = (1/2)b z = 1 5 Factorize (i) 4x29y216z212xy–24yz–16xz (ii) 2x2y28z2–2√2xy4√2yz–8xz Solution

Ncert Solutions For Class 9 Maths Chapter 2 Polynomials

Get RS Aggarwal And V Aggarwal Solutions for Class 9 Chapter Polynomials here BeTrainedin has solved each questions of RS Aggarwal And V Aggarwal very thoroughly to help the students in solving any question from the book with a team of well experianced subject matter experts Practice Polynomials questions and become a master of concepts All solutions are explained using stepEx 25 Class 9 Maths Question 12 Verify that x 3 y 3 z 33xyz = (x y z)(x y) 2 (yz) 2 (zx) 2 Solution We have, x 3 y 3 z 3 – 3xyz = (x y z) x 2 y 2 z 2 – xy – yz – zx = (x y z)2x 2 2y 2 2z 22xy2yz 2zx = (x y z)x 2 x 2 y 2 y 2 z 2 z 22xy2yz2zx = (x y z)x 2 y 2 – 2xy yThis algebraic identity can be written in the following form too ( a − b) 3 = a 3 − b 3 − 3 a 2 b 3 a b 2 Generally, the a minus b whole cubed algebraic identity is called by the following three ways in mathematics The cube of difference between two terms identity or simply the cube of difference identity The cube of a binomial formula

 Ex 25, 9 Verify (i) x3 y3 = (x y) (x2 – xy y2) LHS x3 y3 We know (x y)3 = x3 y3 3xy (x y) So, x3 y3 = (x y)3 – 3xy (x y) = (x y)3 – 3xy (x y) = (x y) (x y)2 – 3xy) Using (ab)2 = a2 b2 2ab = (x y) (x2 y2 2xy) – 3xy = (x y) (x2 y2 – xy) = (x y) (x2 xy y2) = RHS RHS (x y) (x2 – xy y2) Hence proved Ex 25, 9 Verify (ii) x3 y3 = (x y) (x2 xy y2) LHS x3 y3 We know (x y)3 = x3 y3 3xy (x yThe purpose of this unit is to think deeply and critically about personal identity by analyzing characters in texts and making connections to themselves This unit introduces students to literary analysis, promotes creative writing, and supports structured conversations Teachers are encouraged to start of the school year with the 9th grade5 Classify the following as linear, quadratic and cubic polynomials ∵ The degree of x 2 x is 2 ∴ It is a quadratic polynomial ∵ The degree of x – x 3 is 3 ∴ It is a cubic polynomial ∵ The degree of y y 2 4 is 2 ∴ It is a quadratic polynomial ∵ The degree of 1 x is 1

We already have an identity for (x y) 3 So, let's try to derive the identity x 3 y 3 using the identity for (x y) 3 Let's first try to understand this geometrically Let's join our cubes as shown above We arranged both cubes in such a way to convert it into a cube as shown aboveThey have the same value for all values of \ (xNCERT Solution For Class 9 Maths Chapter 2 Polynomials Exercise 25 Page 48 1 Use suitable identities to find the following products Here, the identity, 3 (x y) = x 3 y 3 3xy (x y) is used (ii) 8a 3 –b 3 –12a 2 b6ab 2 Solution The expression, 8a 3 –b 3 −12a 2 b6ab 2 2can be written as (2a) –b 3 –3

X Y 3 Identity Class 9 Novocom Top

Cbse 8 Math Cbse Algebraic Expressions And Identities Ncert Solutions

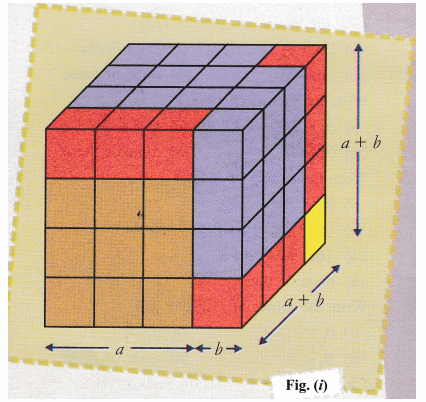
Materials Required A set of 56 cubes each has dimensions (1 x 1 x 1) cubic unitUsing the above identity, the equation x 6 − y 6 can be factorised as follows x 6 Class 9 Maths Chapter 3 Unit 2 163 Qs > Related questions Factorize the following expression 8 x 3(x 3) (x – 3) = x 2 – 3 2 = x 2 – 9 Problem Solve (x 5) 3 using algebraic identities Solution We know, (x y) 3 = x 3 y 3 3xy(xy) Therefore, (x 5) 3 = x 3 5 3 3x5(x5)

Ncert Solutions For Class 9 Maths Chapter 2 Polynomials Exercise 2 5

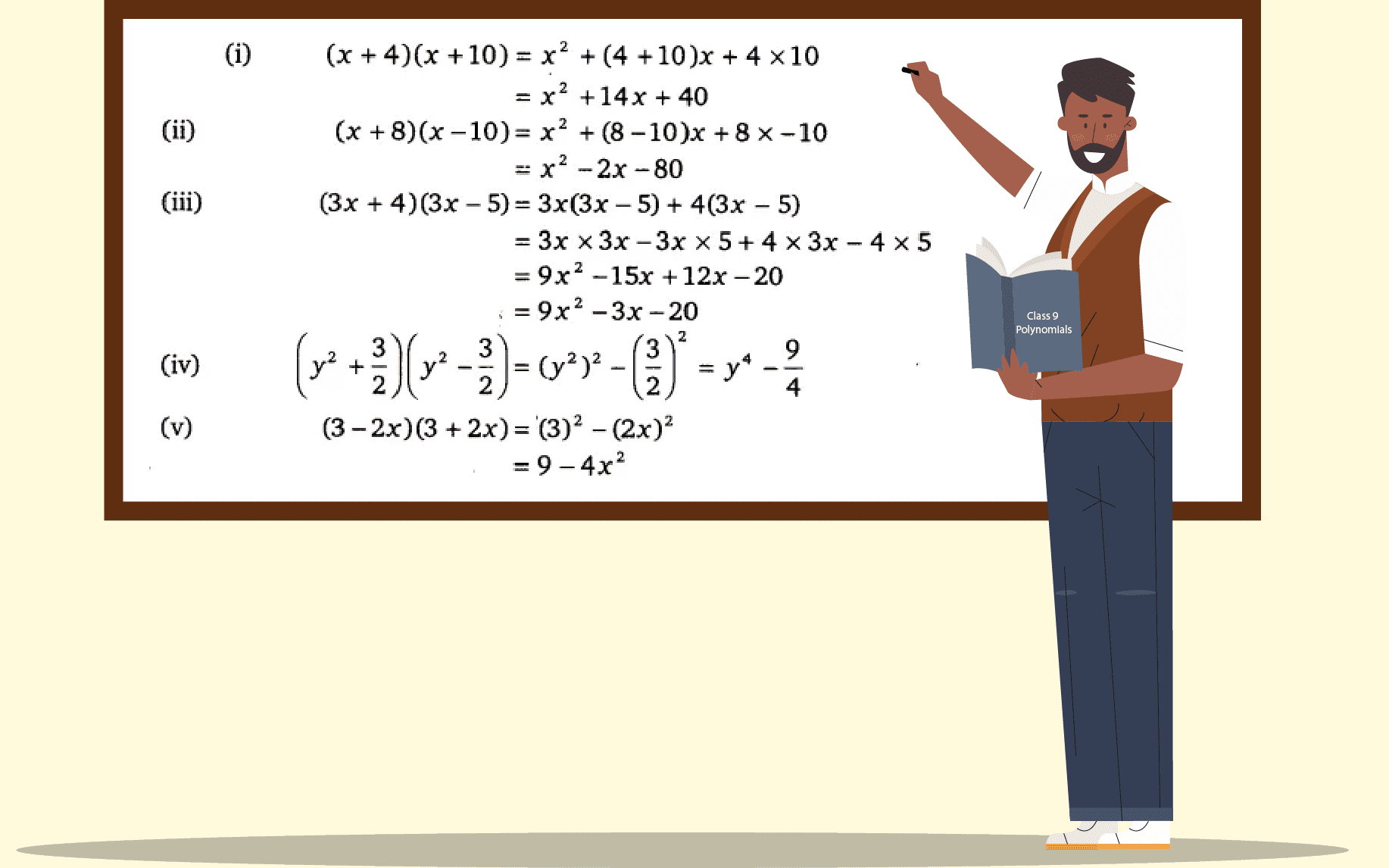
Class 9 Polynomials Study Notes And Important Questions Leverage Edu

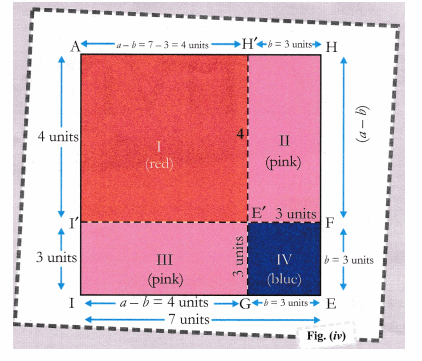
3 EQUIVALENCE RELATIONS 34 and since each of x−x0 and y−y0 is an integer (by definition of R), (x−x0)(y−y0) is an integer Thus, (xy)R(x0 y0) Exercise 321 In the example above, show that it is possible to have xRx0 and yRy0, but (xy)˚R(x0y0) Exercise 322 CBSE Class 9 Maths Lab Manual – Algebraic Identity (a 3 b 3) = (a b) (a 2 – ab b 2) Objective To verify the identity a 3 b 3 = (a b) (a 2 – ab b 2) geometrically by using sets of unit cubes Prerequisite Knowledge Volume of cube = (edge) 3;Example 2x² 1, x – 3, –3/2(y) x Trinomial A polynomial having three terms is known as trinomial Example x² 2x 2 Classification of Polynomials Based on the Degrees of Its Variable Linear polynomial A polynomial having degree one is known as linear polynomial

Ncert Solutions For Class 9 Maths Chapter 2 Polynomials In Pdf

Ncert Solutions Class 9 Maths Chapter 2 Exercise 2 5 Access Free Pdf

(a)x39 x2 23x15 (b) x36 x2 11x6 Q3 Factorize the following by using a suitable identity (a) 4x2 12xy 9y2 (b) 2a5 – 54 a2 (c) 22x3 3 3 y3 (d) x5 x (e) x6 – y6 (f) (ab)3 (bc)3 (ca)3 (f) x8y8 (g) 27x3135x2 225x 125 Q4 Evaluate the following using a suitable identityClass 9 RD Sharma Solutions Chapter 4 Algebraic Identities Ex 43 Question 1 Find the cube of each of the following binomial expressions Solution Question 2 If a b = 10 and ab = 21, find the value of a 3 b 3 Solution a b = 10, ab = 21Problem Solve (x 3) (x – 3) using algebraic identities Solution By the algebraic identity, x 2 – y 2 = (x y) (x – y), we can write the given expression as;

Class 9ncert Solutionschapter 2 Polynomialsexercise 2 5 Solve All Questions And Give Me Answersplease Brainly In

Algebraic Identities Rd Sharma Class 9 Solutions Exercise 4 5

 9 (x y) 3 = x 3 y 3 3xy (x y) = x 3 3x 2 y 3xy 2 y 3 10 (x y) 3 = x 3 y 3 3xy (x y) = x 3 3x 2 y 3xy 2 y 3 11 x 3 y 3 z 3 3xyz = (x y z) (x 2 y 2 z 2 xy yz zx) 12 x 2 y 2 = ½ (x y) 2 (x – y) 2 13 xy = ¼ (x y) 2 (x – y) 2 14 x 2 y 2 = (x yEq1) where E ⁡ X {\displaystyle \operatorname {E} X} is the expected value of X {\displaystyle X} , also known as the mean of X {\displaystyle X} The covariance is also sometimes denoted σ X Y {\displaystyle \sigma _{XY}} or σ (X , Y) {\displaystyle \sigma (X,Y)} , in analogy to variance By using the linearity property of expectations, this can be simplified to the expected valueHi everyonein this video, I tell you about " x^3y^3=(xy)(x^2xyy^2) "?channel link https//wwwyoutubecom/channel/UC7Uui8og_cIpQaH9ItVWM3Q`````

Q Tbn And9gctrh1ypujwtooh8c3vpasyfikri1qchje80vre Ccrxfnsx8i 7 Usqp Cau

Expand 1 X Y 3 Whole Cube Studyrankersonline

 = x 2 y 2 z 2 – 6xyz 8 Question 3 Find the following squares by using the identities (i) (b – 7) 2 Solution (b – 7) 2 Using Formula (x – y) 2 = x 2 y 2 – 2xy Putting x = b & y = 7 = b 2 72 – 2(b)(7) = b 2 – 14b 49 (ii) (xy 3z) 2 Solution (xy 3z) 2 Using Formula (a b) 2 = a 2 b 2 2ab Putting a = xy & bSelina Concise Mathematics Part I Solutions for Class 9 Mathematics ICSE, 4 Expansion All the solutions of Expansion Mathematics explained in detail by experts to help students prepare for their ICSE examsTelanagana SCERT Class 9 Math Solution Chapter 2 Polynomials and Factorisation Exercise 25 Net Explanations All Kinds of Equations Solved Online On comparing it with identity VI where (x – y) 3 = x 3 – y 3 – 3 X x X y (x – y) we get, x = 1, y = 4a ∴ (1 – 4a) 3 = 1 – 64a 3 – 12a 48a 2

Ncert Solutions Class 8 Mathematics Algebraic Expressions And Identities

Download Free Rd Sharma Maths Solutions For Class Ix Factorization Of Algebraic Expressions Chapter 5 Pdf

We shall use the identity xy x y = x 2y 2 Here By applying in identity we get Hence the value of is (iv) The given expression is We have So we can express and in the terms of 100 as We shall use the identity xy x y = x 2y 2 Here By applying in identityClass 9 Maths Polynomials Algebraic Identities Algebraic Identities Algebraic identity is an algebraic equation that is true for all values of the variables occurring in it ( x y) 2 = x2 2 xy y2 ( x – y) 2 = x2 – 2 xy y2 x2 – y2 = ( x y) ( x – y) ( x a) ( x b) = x2 ( a b) x ab (x y z) 2 = x 2 y 2 z 2 2xy 2yz 2zxSelina solutions for Concise Mathematics Class 8 ICSE chapter 13 (Factorisation) include all questions with solution and detail explanation This will clear students doubts about any question and improve application skills while preparing for board exams The detailed, stepbystep solutions will help you understand the concepts better and clear your confusions, if any

Algebraic Identities Of Polynomials A Plus Topper

Standard Identities Of Binomials And Trinomials Equations Examples

We shall use the identity xy x y = x 2y 2 Here By applying in identity we get Hence the value of is (iv) The given expression is We have So we can express and in the terms of 100 as We shall use the identity xy x y = x 2y 2 Here By applying in identityState whether the following statements are true or false Give reasons to justify your answers (a) The degree of polynomial 5 x5 6 x4 8 x2 is 4 (b) The algebraic expression is a polynomial (c) The polynomial is a quadratic trinomial Using the long division method, determine the remainder when the polynomial 4 x5 2 x4 x3 4 x2 7Polynomial Identities When we have a sum (difference) of two or three numbers to power of 2 or 3 and we need to remove the brackets we use polynomial identities (short multiplication formulas) (x y) 2 = x 2 2xy y 2 (x y) 2 = x 2 2xy y 2 Example 1 If x = 10, y = 5a (10 5a) 2 = 10 2 2·10·5a (5a) 2 = 100 100a 25a 2

Ncert Solutions For Class 8 Maths Chapter 9 Algebraic Expressions And Identities In Hindi

Ncert Solutions For Class 9 Maths Chapter 2 Polynomials In Pdf

Volume of cuboid = I x b x h;Polynomials Exercise 25 Part 1 Question 1 Use suitable identities to find the following products (i) `(x 4)(x 10)` Answer Given, `(x 4)(x 10)` We know that, `(x a)(x b) = x^2 (a b) x  Algebraic Identities Polynomials, Class 9, Mathematics EduRev Notes is made by best teachers of Class 9 This document is highly rated by Class 9 students and has been viewed times

If X Y 12 And Xy 27 Then Find The Value Of X3 Y3 Polynomials Maths Class 9

Ncert Solutions For Class 9 Maths Chapter 2 Polynomials Exercise 2 5

 Solution (3x– 4y) 3 is of the form Identity VII where a = 3x and b = 4y So we have, (3x – 4y) 3 = (3x) 3 – (4y) 3 – 3(3x)(4y)(3x – 4y) = 27x 3 – 64y 3 – 108x 2 y 144xy 2 Example 5 Factorize (x 3 8y 3 27z 3 – 18xyz) using standard algebraic identities Solution (x 3 8y 3 27z 3 – 18xyz)is of the form Identity Ex 25, 13 If x y z = 0, show that x3 y3 z3 = 3xyz We know that x3 y3 z3 3xyz = (x y z) (x2 y2 z2 xy yz zx) Putting x y z = 0, x3 y3 z3 3xyz = (0) (x2 y2 z2 xy yz zx) x3 y3 z3 3xyz = 0 x3 y3 z3 = 3xyz Hence proved Evaluate the following using suitable identities (i) (99) 3 (ii) (102) 3 (iii) (998) 3 Solution (i) (99) 3 = (100 – 1) 3 Identity (x – y) 3 = x 3 – y 3

Cbse Class 9 Maths Lab Manual Algebraic Identity A B 2 2ab B2 Cbse Sample Papers

Use A Suitable Identity To Get Each Of The Following Products I

 Here, Right hand side = Left hand side which means that (a3) (a3) is an identity Using Activity Method In this method, the algebraic identity is verified geometrically by taking different values of a x and yThe perfect cube forms ( x y) 3 (xy)^3 (xy)3 and ( x − y) 3 ( xy)^3 (x −y)3 come up a lot in algebra We will go over how to expand them in the examples below, but you should also take some time to store these forms in memory, since you'll see them often ( x y) 3 = x 3 3 x 2 y 3 x y 2 y 3 ( x − y) 3 = x 3 − 3 x 2 y 3Example 12 Factorise the following (i) 21x2y3 27x3y2 (ii) a3 – 4a2 12 – 3a (iii) 4x2 – x 25 (iv) 2 –9 9 y (v) x4 – 256 Solution (i) 21x2y3 27x3y2 = 3 × 7 × x × x × y × y × y 3 × 3 × 3 × x × x × x × y × y = 3 × x × x × y × y (7y 9x) (Using ab ac = a (b c)) = 3x2y2 (7y 9x) (ii) a3 – 4a2 12 – 3a = a2 (a – 4) – 3a 12 = a2 (a – 4

Algebra Formulas For Class 9 Pdf Download Free Here

Ncert Solutions For Class 9 Maths Chapter 2 Polynomials Ex 2 5 Cbsetuts Com

 Since x − y = 3 xy=3 x − y = 3 implies y = x − 3, y=x3, y = x − 3, substituting this into the given identity gives a x (x − 3) b x c (x − 3) 9 = 0 a x 2 (− 3 a b c) x − 3 (c − 3) = 0 \begin{aligned} ax(x3)bxc(x3)9&=0\\ ax^2(3abc)x3(c3)&=0 \end{aligned} a x (x − 3) b x c (x − 3) 9 a x 2 (− 3 a b c) x − 3 (c − 3) = 0 = 0= (x y)(x 2 y 2 2xy x 2 xy y 2) using identity, (a b) 2 = a 2 b 2 2 ab) = (x y) (3xy) Hence, one of the factor of given polynomial is 3xy Question 18 The coefficient of x in the expansion of (x 3) 3 is (a) 1 (b) 9 (c) 18 (d) 27 Solution (d) Now, (x 3) 3 = x 3 3 3 3x (3)(x 3) using identity, (a b) 3 = a 3 b 3 Polynomials Class 9 Extra Questions Very Short Answer Type Question 1 Factorise 125x 3 – 64y 3 Solution 125x 3 – 6443 = (5x) 3 – (4y) 3 By using a3 – b3 = (a – b) (a 2 ab b 2), we obtain 125x 3 – 64y 3 = (5x – 4y) (25x 2 xy 16y 2) Question 2 Find the value of (x y) 2 (x – y) 2 Solution (x y) 2 (x – y) 2 = x 2 y 2 2xy x 2 y 2 – 2xy

Ncert Solutions For Class 9 Maths Chapter 2 Polynomials Ex 2 5 Cbsetuts Com

110 Class 9 Rd Sharma Solutions Ideas Solutions Sharma Class

Ex 2 5 12 Verify That X3 Y3 Z3 3xyz 1 2 Ex 2 5

5 Extra Questions For Class 9 Maths Chapter 2 With Solution Polynomials Zeroes Remainder Theorem Factorization And Algebraic Identities

Chapter 4 Algebraic Identities Rd Sharma Solutions For Class 9 Mathematics Cbse Topperlearning

Ncert Class 9 Maths Lab Manual Verify The Algebraic Identity A B C A B C 2ab 2bc 2ca Cbse Tuts

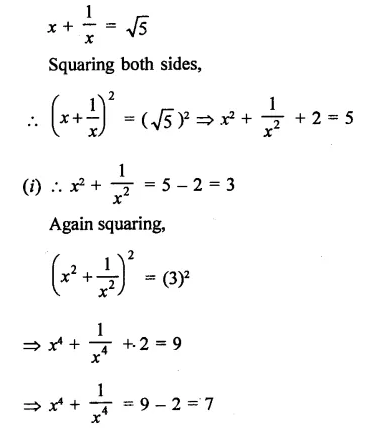
Rd Sharma Class 9 Solutions Chapter 4 Algebraic Identities Ex 4 1

Chapter 4 Algebraic Identities Rd Sharma Solutions For Class 9 Mathematics Cbse Topperlearning

Algebraic Expressions And Identities Class 8 Maths Geeksforgeeks

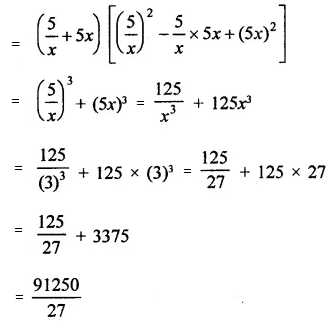
Rd Sharma Class 9 Chapter 4 Algebraic Identities

Cbse Class 9 Maths Lab Manual Algebraic Identity A B 3 A3 3a2b 3ab2 Cbse Sample Papers

How To Verify Algebric Identity X Y 3 X3 3xy X Y Y3 Maths Polynomials Meritnation Com

Example 8 Multiply I X 4 And 2x 3 Ii X Y 3x 5y

Ex 9 4 3 Vi Simplify X Y X 2 Xy Y 2 Chapter 9 Class 8

3

Ex 2 5 9 Verify I X3 Y3 X Y X2 Xy Y2 Ex 2 5

Telangana Scert Class 9 Math Solution Chapter 2 Polynomials And Factorisation Exercise 2 5

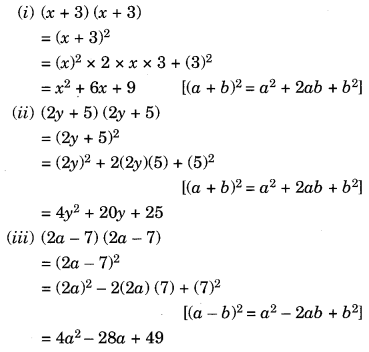
Ncert Solutions For Class 8 Maths Chapter 9 Algebraic Expressions And Identities Ex 9 5 Learn Cbse

Class 9ncert Solutionschapter 2 Polynomialsexercise 2 5 Solve All Questions And Give Me Answersplease Brainly In

Maths Polynomials 9th

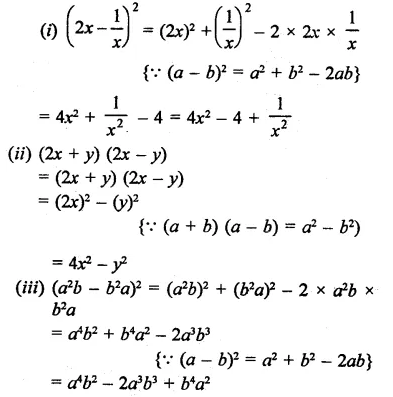
Rd Sharma Class 9 Solutions Chapter 4 Algebraic Identities Ex 4 1

Class 9 Chapter 2 Polynomials Cubic Identities X Y 3 X 3 Y 3 3xy X Y X Y 3 X 3 Y 3 3xy X Y Youtube

Rd Sharma Class 9 Chapter 4 Algebraic Identities

X Y 3 Identity Class 9 Novocom Top

Telangana Scert Class 9 Math Solution Chapter 2 Polynomials And Factorisation Exercise 2 5

1 9m02 4 Cv1 ब ज य सर वसम क V Alegebraic Identity V Youtube

Ncert Solutions For Class 9 Maths Chapter 2 Polynomials

Standard Identities Of Binomials And Trinomials Equations Examples

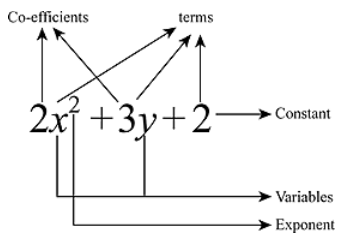
Revision Notes For Maths Chapter 2 Polynomials Class 9th Askiitians

Tell Me All Identities Of Chapter Polynomial Class9 Brainly In

Example 11 Using The Identity I Find I 2x 3y 2 Ii 103 2

Telangana Scert Class 9 Math Solution Chapter 2 Polynomials And Factorisation Exercise 2 5

Class 9 Maths Formulas Download Class Ix Maths Formulae Pdf Embibe Exams

Selina Concise Mathematics Class 8 Icse Solutions Chapter 12 Algebraic Identities Cbse Tuts

State All The Algebraic Identities From Polynomials Maths Meritnation Com

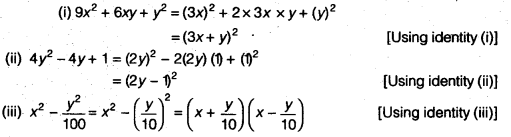
Ncert Solutions For Class 9 Maths Chapter 2 Polynomials Ex 2 5

Algebraic Identities Of Polynomials A Plus Topper

Cbse Class 9 Algebraic Identities Offered By Unacademy

Rd Sharma Class 9 Chapter 4 Algebraic Identities

Rd Sharma Class 9 Solutions Algebraic Identities Exercise Flickr

Ncert Solutions For Class 9 Maths Chapter 2 Polynomials In Pdf

Ex 9 5 3 Find The Squares By Using Identities I B 7 2

Important Questions For Cbse Class 9 Maths Chapter 2 Polynomials

Chapter 4 Expansion Selina Concise Mathematics Part I Solutions For Class 9 Mathematics Icse Topperlearning

Ex 9 3 3 Find The Product I A 2 X 2a 22 X 4a 26 Ii 2 3 Xy

Ncert Solutions For Class 9 Maths Exercise 2 5 Chapter 2 Polynomials Study Path

Mathematics Class 9th Chapter 2 Solution

Algebraic Expressions And Identities Class 8 Maths Geeksforgeeks

Identity Mathematics Wikipedia

Algebraic Identities Of Polynomials A Plus Topper

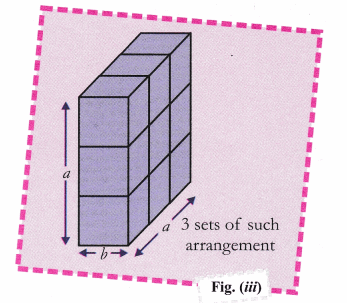
Cbse Class 9 Maths Lab Manual Algebraic Identity A B 3 A3 3a2b 3ab2 Cbse Sample Papers

Rd Sharma Class 9 Solutions Chapter 4 Algebraic Identities

Algebraic Identities Of Polynomials A Plus Topper

Notes Of Ch 2 Polynomials Class 9th Math

Ncert Solutions For Class 8 Maths Chapter 9 Algebraic Expressions And Identities

Questions On Algebraic Expressions Algebraic Identities Algebraic Formulas

Polynomials Class 9 Maths Notes With Formulas Download In Pdf

Ncert Solutions For Class 9 Maths Chapter 2 Exercise 2 5 Polynomials

Polynomials Class 9 Extra Questions Maths Chapter 2 Learn Cbse

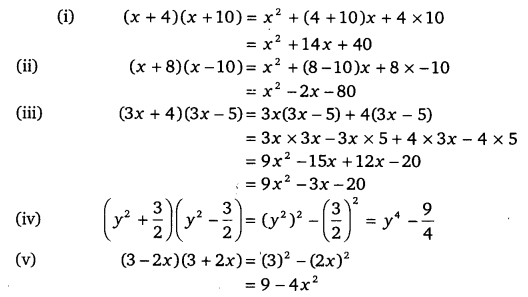
Ncert Solutions For Class 9 Maths Chapter 2 Polynomials Ex 2 5 Cbsetuts Com

Use A Suitable Identity To Get Each Of The Following Products I

Expand Each Of The Following Using Suitable Identities I X 2y 4z 2 Ii 2x Y Z Youtube

Ncert Solutions For Class 9 Maths Chapter 2 Polynomials Exercise 2 5

If X 3 A N D Y 1 Find The Values Of Each Of The Using Identi

X Y 3 Identity Class 9 Novocom Top

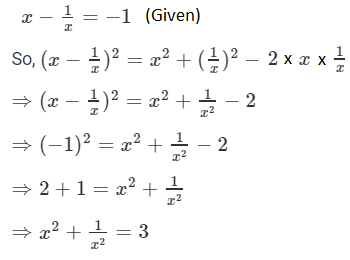
Rd Sharma Class 9 Chapter 4 Algebraic Identities

Important Questions For Class 8 Maths Chapter 9 Algebraic Expressions And Identities Free Pdf

Ncert Solutions For Class 9 Maths Chapter 2 Exercise 2 5 Mathongo

Ncert Solutions Class 9 Maths Chapter 2 Exercise 2 5 Access Free Pdf

Ncert Solutions For Class 9 Maths Chapter 2 Polynomials

1

Kseeb Solutions For Class 9 Maths Chapter 4 Polynomials Ex 4 5 Kseeb Solutions

Ncert Solutions For Class 8 Maths Chapter 9 Algebraic Expressions And Identities Ex 9 5 Cbsetuts Com

Use Suitable Identities To Find The Following Products I X 4 X 10 Ii X 8 X 10 Ii Youtube

Rd Sharma Class 9 Solutions Algebraic Identities Exercise 4 3 14 Rdsharmaclass9 Class9solutions Rdsharmaclass9solutions R Solutions Math Notes Class

Ncert Solutions For Class 8 Maths Algebraic Expressions And Identities Ex 9 4 Algebraic Expressions Class 8 Expressions

Polynomials Important Questions Of Identities Algebraic Identities Class 9 Oda Class Youtube

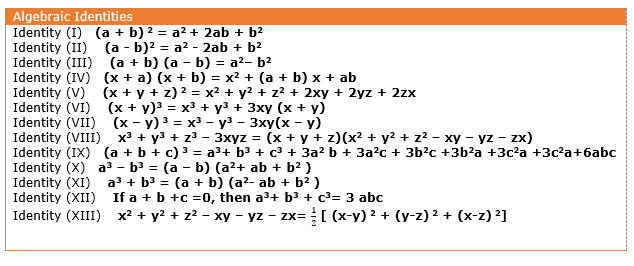
All Useful Algebraic Identities With Proof Examples Physicscatalyst S Blog

1

Ncert Solutions For Class 8 Mathematics Chapter 9 Algebraic Expressions And Identities Exercise 9 5

Rd Sharma Class 9 Solutions Chapter 5 Factorisation Of Algebraic Expressions Exercise 5 1

All Identities Of Class 9 Maths Ch 2 Polynomial Brainly In